Leave a Comment
Leave a Comment
Geronimo and the Cubic Equation
This picture of Geronimo, Bedonkohe Apache medicine man and leader, was taken in 1887, probably after his arrival at Fort Pickens, Pensacola, Florida. It is linked to his biography.
When WW II paratroopers shouted "Geronimo!" exiting an airplane, they were invoking Apache courage, not the name of sixteenth century polymath, Geronimo Cardano. No one has probably ever made that mistake, but it would be understandable. If Cardano had associated with his father's friend, Leonardo Da Vinci, resulting in him gaining access to one of the latter's not-in-his-lifetime-but-dreamed-of inventions, the parachute, he might well have tried it out. He was apparently that kind of guy. Cardano was a prolific author, demonologist, cryptographer, philosopher, mathematician, gambler, doctor, geologist, and heretic who was imprisoned by the Inquisition for casting the horoscope of Jesus Christ.
Gerolamo Cadano, eccentric and confrontational physician, mathematician, scholar, made first systematic use of negative numbers, and published the first universal solution to the cubic equation.
Names take slippery passage over the slopes of time. Geronimo, the Mescalero Chiricahua, was named Goyahkla, which may have meant "One Who Yawns," or, if pronounced Gothalay, may have meant "intelligent, shrewd, and clever." The Mexicans dubbed him "Geronimo," perhaps because they couldn't get their Spanish-speaking palettes around the Apache phonemes. Geronimo Cardano may have been called Gerolamo, an alternate Italian spelling/pronunciation. The French called him "Jerome," and he himself claimed the Latin version, Hieronymus Cardanus, in his memoir. Language, being made of sound and sense, bends a little as it goes from ear to ear, and era to era, which makes it all the more remarkable that the concepts it encodes, and transmits through the ages, arrive in our own time mostly intact.
This link is to a PDF translation of Gerolamo Cardano's opus, "Ars Magna," or The Rules of Algebra. Be patient, it takes a moment to download.
Cardano sent a lot of concepts our way, and many of them are in a more universal language than his native Italian, or his acquired Latin, Greek or French. He was, among many things, a mathematician, and gets credit for publishing the tangled solution to a problem malevolent to high school algebra students, and annoying enough to college undergrads that most of them avoid it. Many consider it impossible, and I believe I have even read such an assertion in a textbook someplace, although the reference eludes me now. Cardano solved the cubic equation.
This Babylonian tablet, known as Plimpton 322, written around 1800 BCE in Mesopotamia, is currently at Columbia, and is among the earliest representations of the Pythagorean Theorem. It links to a short history of algebra.
The historic roots of algebra, and the understanding of cubic equations, grew first in ancient Babylon, circa 20th century BC, were nourished in India, came up in Greece, where mathematics was mostly geometry, and finally flowered in the Arabic world, and Europe. Algebra is a precise way of thinking about, and discovering, general rules about unknown quantities. When the thing unknown can be expressed as simple arithmetic, multiplication and addition involving itself and known values, it can be drawn on a sheet of graph paper as a straight line, and is called a linear function.
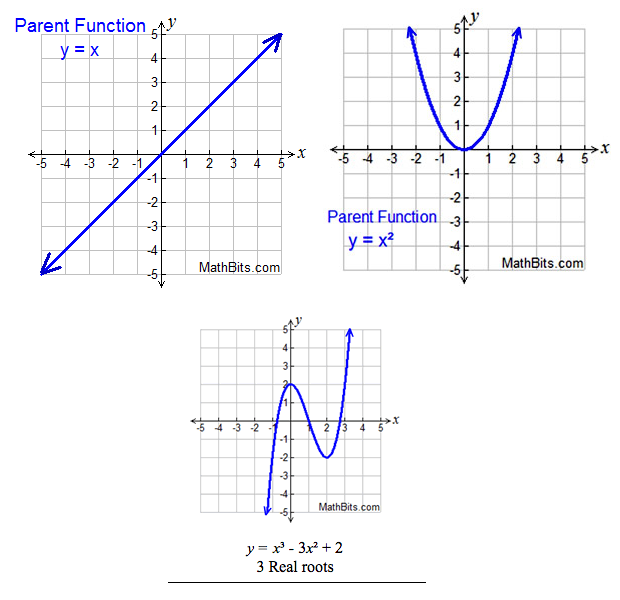
These graphs include a linear function, upper left, quadratic (squared) function, upper right, and a cubic function, lower center. The picture links to a brief description of linear, quadratic and cubic functions.
If the thing unknown gets multiplied by itself, in addition to known quantities, it appears on graph paper as a curve. Multiplying something by itself is represented in mathematical notation by an exponent. If two iterations of the unknown are multiplied together, it is called "squaring," and if three iterations, it is called cubing. A cubic equation is a formula for defining an unknown in which the unknown is cubed, three iterations of the unknown multiplied together.
Brahmagupta (598-668 CE) is credited with developing the quadratic equation, infamous among high school algebra students, as well as being among the first to formalize use of zero as a number. The link is to a short biogrpahy.
High school algebra students learn how to solve quadratic equations, those in which the unknown is squared, and can pretty readily understand the reasoning behind the process. The basic mathematics were published and probably discovered by the Indian mathematician, Brahmagupta (598-665 CE).
Cubic equations are more difficult and students can get all the way through college without realizing there is a general way of solving them. The history of cubic equations goes back to Babylon, around 2000 BC. The Babylonians had tables of cubes and cube roots, and evidently thought about the problem, but there is no evidence they had a solution. The Greeks could solve some special cases of cubic equations, as did the Chinese. Persian poet Omar Khayyam (1048-1131), think The Rubaiyat, wrote "Treatise on Demonstration of Problems of Algebra" (1070), and paved an intellectual path toward the solution of cubics.
Omar Khayyam cycles in and out of fashion among American college students, every-other generation rediscovering the beauty and grace of his Rubaiyat. Few suspect the full scope of his intellecutual chops, and fewer yet have heard of his facility with mathematics, and his contributions to solving the cubic. After all, one is allowed to be content with such as appears to the right.
Incidentally, for students lost in the maze of geometry, algebra, analytic geometry and geometric algebra, take heart in knowing that as long ago as the eleventh century, Khayyam asserted the unity of mathematics: " Whoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved by propositions five and six of Book two of Elements." Plow on, bewildered student, the picture will appear.
This 7th Verse of the Rubaiyat is a favorite of many, often quoted, variously understood, and is linked to some reflections on the famous poem, and the meaning of it all, by one who discovered the mysterious tent maker during the 60s.
It took from 2000 BC to the sixteenth century CE, for the world's best mathematical minds to crack the cubic equation. The heavy lifting was done by Scipione del Ferro (1465-1526), who discovered a trick for solving a specific class of cubic equations. If he'd known about negative numbers, which were invented in China ca 200 BC, systematized in tenth century Persia, but not accepted in Europe until the 17th century, he might have realized that his special case could be generalized to all cubic equations.
Angelo Paratico explains his theory in the above link.
While we're digressing about literary matters, it's a good time to mention that some people, ever on the lookout for the Bard's sources, suspect William Shakespeare may have heard of Gerolamo Cardano, and used him as inspiration for Prospero in The Tempest.
Scipione del Ferro was apparently the first person to find a general solution to what is called the depressed cubic equation (missing the squared term, not emotionally disabled). Here is an account of the matter, including a quote from Gerolomo Cardano who later published the result. Notice the assertion that Scipione did not know how to generalize the depressed case to the general. This seems to be a point often missed by modern biographers.
The drama of intrigue and betrayal (soap opera at its best) enters the cubic equation story after del Ferro's death. He kept his method a secret, but confided it to a student, Antonio Fiore, just before he died. Nicholas Fontana, known as Tartaglia, Stammerer, because of a childhood wound received from a French soldier during the Massacre of Brescia, seems to have independently discovered del Ferro's method. Tartaglia was a self-taught engineer, mathematician, scholar, bookkeeper, who received a challenge from del Ferro's student, Fiore, to solve some cubic equations. Such challenges seem to have been a blood sport in those days, and Fiore probably thought he had a sure thing because of knowing del Ferro's secret method. Despite this advantage, Fiore lost to Tartaglia, elevating the latter to heights of academic acclaim.
Tartaglia's dispute with Cardano involved strong feelings. Here is a taste of how he and Cardano saw things. There will be an embedded link to a biography of the man.
Now enters Geronimo, Gerolamo Cardano. Cardano persuaded Tartaglia to divulge his cubic equation secret, by promising he would not pass it on. Cardano later learned of del Ferro's earlier work, declared himself unconstrained by his promise, and published the work, attributing it to del Ferro, not Tartaglia. Tartaglia cried foul, and challenged Cardano to a contest. Cardano refused, but later, Cardano's student, Lodovico Ferrari, accepted on Cardano's behalf. Poor Tartaglia lost to Ferrari which apparently doomed his reputation and income. These were serious matters. Today, the generalized solution of the cubic equation is easily found in textbooks, and online, and is attributed to Cardano. Henry Ford famously said, "History is bunk." Sometimes he seems prescient.
This image of the cover of the 1539 publication of Cardano's "Practica Arithmetice," links to the Wolfram discussion of the derivation of the cubic formula.
If you're inclined to understand what all the fuss was about, you can follow the development of the cubic equation solution, with just a little effort. If you want to convince yourself you could have thought of it yourself, that will take more effort, but can be done.
Any quadratic equation (involving squared unknowns) can be solved by the quadratic formula, readily developed in any beginner's algebra text. A similar formula, except more complicated, solves the cubic equation (involving cubed unknowns).
To derive the quadratic formula involves a single, pretty simple trick called "completing the square." Deriving the cubic formula involves two tricks, one of them non-obvious, and the other devilish in its double-backs and intricacies, but understandable with a little effort.
Any cubic equation can be written like this, where "x" is the unknown value, and the other letters, called coefficients, stand for any, arbitrary number.
This is one of many pictures appearing on the public domain review pages dedicated to Goyahkla. The link is to the cache of materials about Geronimo held in the Public Domain records, including a link to his autobiography.
Trick number one is to notice that that a clever way of rewriting the unknown, x, expressing it as a second unknown, y, defined by a carefully selected equation, x=y-(a/3), almost magically turns the generalized cubic equation into the "depressed" equation having no squared term. This form of the cubic equation is the one for which del Ferro, and apparently Tartaglia, discovered a generalized solution.
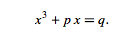
Where:
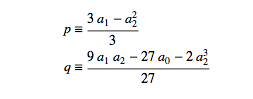
Francois Viete (1540-1603) was a French lawyer who, in his spare time, developed general mathematical expressions relating polynomial coefficients to their roots. His formulas are the ones used today to derive the solution for the cubic equation, although, of course, they were unknown in their current generality to Cardano.
To derive Tartaglia's, and Cardano's, solution, another, more difficult trick is needed. This is commonly called Vieta's substitution, after Francois Viete (Franciscus Vieta, 1540-1603), who generalized some properties of polynomials in what are called Vieta's formulas. Since he developed these results after the work of del Ferro, Cardano et al, it is obvious Vieta did not influence them. Those gentlemen seem to have developed, on their own, a special case of Vieta's more generalized formulas.
In any case, by making something like Vieta's substitution into the cubic equation, as restated above after the first little trick, Cardano was able to reduce the cubic equation to a quadratic (squared unknown) equation, for which the quadratic formula could be used.
If you'd like to follow this process in detail (and who wouldn't?) the Wolfram website linked above gives us the essential steps. If you'd like to understand something about the workings of a mind that dreams up this kind of stuff, the picture at right links to some motivational noodling by someone who's been there. Anyone with pretty good pattern recognition skills, and a willingness to direct them toward this problem, could probably do something similar to what Cardano and his buddies accomplished, but remember, you're working with advantages they didn't have. You have modern algebraic notation, knowledge of negative and complex numbers, plus ready access to much of the world's information. Imagine dreaming this stuff up when mathematical treatises were written in verse, intermingled with religious convictions, and everyday life was mostly a scramble for food, shelter and safety.
Now that we've veered closer to something like real mathematics, you may wonder what inspired such mental sleight of hand in those Renaissance sages. Language fetches us to long-ago worlds. We read Yeats and feel the Irish chill, and see his sylphish, verdant environs. We read Shakespeare and hear the boisterous crowds around torchlit stages, howling as Lear rants and Hamlet dithers. We read Homer and smell the campfires on the beaches at Troy.
Dr. Gowers, linked above, returns with another, even more insightful analysis. Click the link at left and absorb his new path to the cubic solution. This time he uses matrices, which some of us don't like, but never mind. They seem so intuitive; you might be tempted to pull down that old textbook. Resist. His discussion is short. Read it a few times. Let it conjure the campfires and crowds of times past. You may, in picking the meaning out of his words, glimpse a vision of the inside of del Ferro's mind.
The link is to Amazon's sample of the book's contents. You may read a few pages, or buy the book from them.
The link is to a book store where you may purchase Cardano's book on gambling, or sample a few pages.
By the way, Cardano wrote several books. He was a professional gambler and wrote an early treatise on probability in "Book on Games of Chance," and a memoir called, "The Book of My Life." His father, Fazio, was also a mathematician, a college professor and a practitioner in what we might today call alchemy, heremetical science, and he is said to have been always in the company of a spirit with whom he conversed. He was a friend of Leonardo da Vinci.
If we consider, the amazing difficulty in passing a simple declarative statement between two people, slightly separated in space, without misunderstanding, and factual confusion, it can seem confounding in the extreme to realize we can replicate in our own minds, the ideas and thought processes of people who lived centuries, even millenia ago, and who spoke langages that have never been heard by any living person. Language is circular, recursive, and plastic, but somehow our minds know what to do with it. How we do it, is a mystery that outlives the mystery of the cubic equation.
WILLIAM B. BREUER landed with the first assault waves in Normandy on D-Day, then fought across Europe. Later, he founded a daily newspaper on a string in Rolla, Missouri, and after that, a highly successful public relations firm in St. Louis, Missouri. He has been writing books full time since 1982, twelve of which are now out in paperback, and eight of which have become main selections of the Military Book Club.
Who in the world cares about Geronimo?
