Moderately Big Numbers

Modern humans, people we'd recognize, have been around about 300 thousand years. One of them left a record about 20,000 years ago of things counted: "tally marks" scratched out on a baboon's fibula, now called the Ishango Bone. This and other tally sticks are presumed to represent ancient books of accounts. Ishango is the earliest number conception in the human record.

The abstraction of tally marks to the modern concept of universal quantity agents (numbers) is traced to Sumeria about 6,000 years ago. About 5,000 years ago the Egyptians broadened number utility from counting real things (e.g. sheep) to counting made-up things (e.g. cubits on the side of a pyramid), which enabled the science of measurement and led to the concept of more sophisticated numbers (fractions and irrationals) to fill the space between the counting numbers on measuring sticks.

Complex cultural interactions introduced complicated numerical questions, which led to advances in number use. The Sumerians used numerical symbols. The Egyptians invented unique symbols for different numbers, and the Greeks developed an early logical formalism linking abstract numbers and physical spaces. Zero occurred to the Sumerians, and the Mayans, and others, but the idea of including it in calculations came from India about 1500 years ago.

Most humans have needed very few numbers over the millenia . The number "one" was the first to get a name, and some cultures, right down to our era, met their numeracy needs with that alone (or less). Lately, those of us in the most complex cultures need moderately large numbers. That can be a problem.

We get along well with numbers in the ten to twenty range (matching the digits we carry around with us). With a little practice we're fluent in the thousands, and tens of thousands, and can toss in the notional million.

Our politicians, not required to be great thinkers, contrive national expenditures in the billions, and trillions, and most of us need a moment to stretch our intuitions over such numbers. Also, there are the astronomical quantities involved in science, and although they may seldom seep into our daily lives, it's hard to live in a world in which almost everything we hear about is obscured in some innumerate black hole.

Sometimes we use money as the vehicle for conceiving overly big numbers. It can work for a while. For example, suppose you found a way to earn $1000 plus living expenses per day. It may be well beyond our employment prospects, but it is imaginable. Suppose you made that amount for 100 days. You'd have $100,000.

Now, suppose you maintained that earning prowess for 1000 days, nearly three years. You'd have a million dollars. So far, so good. A hundred days for $100,000 and nearly three years for a million. All understandable. What about a billion? Uh oh. Even with our barely imaginable salary we'd spend almost three millennia (2740 years) becoming a billionaire.

If Homer had wrangled a book contract for his Trojan War tales, he possibly could have about a billion socked away by now. How about a trillion? That would take a thousand times longer.

Consider Donald Johansonh's Lucy, a pre-modern hominid who lived about three million years ago. If she'd set up a toll gate in the Awash Valley for the human migration out of Africa, with some aggressive pricing, and a little tweaking of the emigration trails, she might have saved up a trillion dollar nest egg by now.

This analogy won't go much further. The next long term entrepreneur would have lived three billion years ago when Prokaryotes became the first life forms on earth beneath a recently acquired moon. Who'd pay them a thousand a day?

Instead of money, let's switch to space for our analogy. There's a lot more of it, and we can pretty easily imagine it because we've seen pictures of it going out pretty far.

This idea probably came from the book, “The Anthropic Cosmological Principle,” by John D. Barrow and Frank J. Tipler, but the exact reference is momentarily elusive, pending a re-reading of the book.

We'll need some shorthand lingo borrowed from high school science class. 10³ means a 1 followed by 3 zeros, also called one thousand. 10⁶ means a 1 followed by 6 zeros, also called one million, and so on.

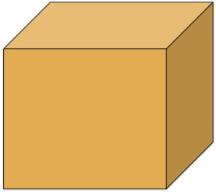
Imagine you had an unlimited supply of tiny ball bearings, one millimeter in diameter. Make them magnets so they stick together. Now string a thousand (10³) of them together on the floor. Next, place a thousand of these strings side by side making a square. That's a million (10⁶). Next, stack a thousand of these ball bearing floor mats on top of each other, making a cube, one meter on a side. That's a billion (10⁹).

So far so good. We're up to a billion and we're comfortable in the living room with our feet propped up on a billion-bearing hassock. Now for a trillion (10¹²). String a thousand of these cubes end-to-end. It makes a rectangle extending out of the living room and down the road a thousand meters (nearly 2/3 of a mile). That's the difference between a billion and a trillion. One is a footrest, and the other is a hike up the road.

Let's see how far this analogy of cubes will take us. Form a square with a thousand of our trillion-ball-bearing rows, and we're up to 10¹⁵, called a quadrillion. We've covered a square kilometer, several city blocks. You might want to note that our bodies contain about 10¹⁴ cells, with as many neuronal connections in the brain. That's about 100 rows of our kilometer square.

Complete the cube made up of one thousand of those quadrillion ball bearing squares and we have a cube a little more than half a mile on a side, extending well up into the FAA's controlled airspace, and we are now at 10¹⁸, also called a quintillion.

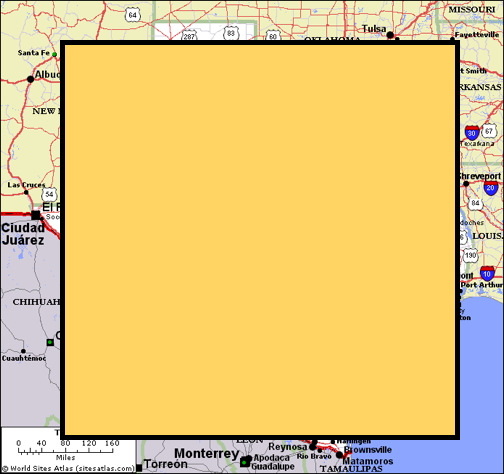
Let's just keep going with our lines, surfaces and cubes. In the next step we get to 10²¹, one sextillion, with a row of cubes extending about six hundred miles down the road. One septillion, 10²⁴, is a six hundred mile square, almost covering the state of Texas. One octillion, 10²⁷, is a six hundred mile cube, allowing Houston to build a stairway three times higher than the International Space Station.

One nonillion, 10³⁰, is a six hundred thousand mile row of cubes extending off the planet to a point about 381,000 miles beyond the moon. One decillion, 10³³, is a square extending around the earth, and out into the asteroid belt. One undecillion, 10³⁶, is a six hundred thousand mile cube engulfing the earth and surrounding space.

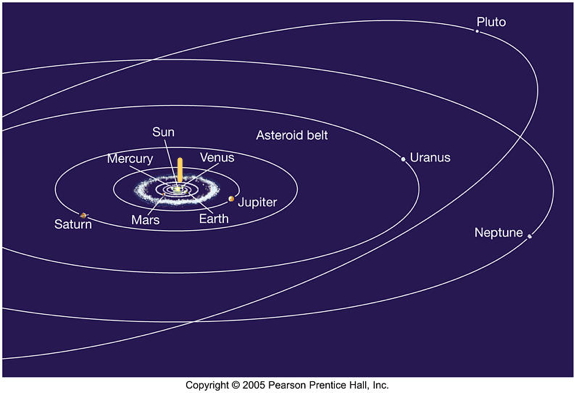
One duodecillion, 10³⁹, is a six hundred million mile row extending past Jupiter to within 200 million miles of Saturn. One tredecillion, 10⁴², completes the square that covers the orbit of Jupiter just inside Saturn. One quattuordecillion, 10⁴⁵, completes the cube inside Jupiter’s orbit. Ten of its rows, 10⁴³, represents the so-called “Shannon number,” the lower bound on the game-tree complexity of chess. This may confirm what you've long believed about chess players.

One quindecillion, 10⁴⁸, is a row extending about 600 billion miles into space, or about one tenth of a light year. That is about 171 times the distance from Earth to Pluto. One sexdecillion, 10⁵¹, completes the 600 billion mile square. One septendecillion, 10⁵⁴, completes the 600 billion mile cube, engulfing the solar system and then some.

One octodecillion, 10⁵⁷, is a row extending about one hundred light years from earth. That’s about a tenth of the distance across our galaxy, the Milky Way. One novemdecillion, 10⁶⁰, is a 100 light year square. One vigintillion, 10⁶³, is a cube encompassing about 512 of what are known as illumination-type G stars.

One unvigintillion, 10⁶⁶, is a row extending about one hundred thousand light years from earth, which takes us across the Milky Way. One duovigintillion, 10⁶⁹, is a square covering a one hundred thousand light year area, nearly all of the Milky Way. One trevigintillion, 10⁷², is a cube filling much of the space inside the Milky Way.

One quattuorvigintillion, 10⁷⁵, is a row extending about 100 million light years from earth, which takes us out beyond the Virgo Cluster of galaxies and three fourths of the way to the Great Attractor, a gravity anomaly in deep space discovered by the Hubble Space Telescope. One quinvigintillion, 10⁷⁸, is a square covering 100 million light years. One sexvigintillion, 10⁸¹, is a cube 100 million light years on a side. This is also the estimated number of atoms in the observable universe. Ten of these cubes would get us a billion light years away, and a hundred would reach out 10 billion light years, where we'd find the Hercules-Corona Borealis Great Wall, the largest structure so far discovered in the universe.

One septenvigintillion, 10⁸⁴, is a row extending 100 billion light years, taking us beyond the observed universe by almost a factor of ten. That’s far enough.

In trying to make sense of large numbers we’ve fallen into a conceptual void with great distances. Still, the method suggests how much bigger each new multiple of one thousand becomes.